Systems World

INDEX

• Thinking
• Systems Thinking
• Cause and Effect Fundamentals
• Using CLMs to Illustrate
• General Approach
• Towards Numerical Analysis
• Modelling Tools - iThink™ / Stella™
• Queuing Models
• Thinking about Market Systems Engineering
• Toyota Assembly Line
• Kaizen at Toyota
• Systems Engineering Cost Models
• The Three Body Problem and Chaos

Thinking

…A precious commodity, and one we employ too seldom, in our daily rush. As the world around us becomes ever more complex — an inevitability — we can either become swept along with the onrushing tide, or take time to think so that we might have some chance of guiding our passage.

But, how to think about such a complex world? One approach is to break the complex world into smaller, more manageable pieces. The argument goes that if we can understand the separate pieces, then we can put our separate understandings together to understand the whole. This is reductionist, or Cartesian (after René DesCartes) Thinking. It works for simple things.

Cartesian thinking fails to address complex problems because, in the process of breaking up the overall concern into parts, the connections and interactions between those parts get lost. Consider a comparison:-

1. If you break a dry-stone wall apart, you end up with a pile of stones, with which you can rebuild the dry-stone wall — nothing lost, and perhaps even something gained in an improved wall
2. Take a human-being apart, perhaps as a surgeon, and you end up with a pile of organs, bones, muscles, sinews...but you can never reconstitute the human being

The difference? The whole human depends on the continued interaction between all the parts — in fact, the parts are all mutually dependent. So it turns out to be with complex systems — they are made up from many interacting, mutually dependent parts. Because of this it is often impractical to conduct experiments on them. Just imagine the social scientist, at the height of the prison riot, saying: "Stop just a tick chaps, I want you all to tell me what your feelings are at this moment."

Systems Thinking

So, what is systems thinking? Fundamentally, of course, it is thinking about some world, or universe of discourse, in terms of open, interacting systems. Which can seem like nailing jelly to a wall in complex situations? So, the practice is growing and spreading of simulating systems behaviour, using simple dynamic, non-linear simulations. Hence:

Systems thinking seeks enlightenment through the creation and exploitation of open, interacting, nonlinear dynamic systems models of problems, situations and phenomena.

Put into simpler terms, a problem, situation or phenomenon is first modelled as interacting systems, such that the model exhibits behaviours that replicate those of the problem, situation or phenomenon. The model is then used as a "learning laboratory," so that various aspects may be changed, augmented, rearranged, etc., to understand and to change behaviour. Finally, it may be possible to propose and test some beneficial changes in the model, with reasonable expectations that corresponding changes in the real world would afford similar benefits. Systems thinking, then, is a way of understanding the complex real world we see about us, of managing its complexity, and of conceiving and testing ways of changing behaviour "in vitro," with a view to implementing similar changes in vivo.

System thinking is systems-scientific, and the models that it engenders are systems theoretic behaviour models. They are, in general, nonlinear because the world they represent is nonlinear. They are also holistic, i.e., the models are of whole systems, without external, unqualified sources and sinks. And they are synthesized without reduction. In systems models, the interactions are as important as the systems

Cause and Effect Fundamentals

So, we need to be able to think about complex issues, partly because we cannot, rationally, use Cartesian methods to "reduce" them, and partly because we cannot conduct controlled experiments upon them. The implications of that are simply this: System Thinking must be rigorous if it is to be both credible and useful. But, is all Systems Thinking rigorous?

There appear to be many different ways of thinking "rationally" — whatever that means! Fundamentally, you can boil them down to a few archetypes. Three of these are shown below:-

1. The figure shows simple, straightforward reductionist thinking at the top. Effect follows upon cause. There is no observable connection between one cause and another.
   • This mode of thinking is favoured by some politicians and accountants, often on ideological grounds, but also because they are unwilling or unable to accommodate the complication that would ensue if they followed the second archetype.
   • System thinkers in this domain use statistics and static models.
2. The second archetype indicates that "one person's effect is another's cause" i.e. that causes and effects form chains like dominoes falling.
   • This is a view held by many engineers and scientists, who believe in a clockwork universe and that, if only they had enough information, they could plot out the whole of time since creation and on into our futures.
   • System thinkers in this paradigm use Influence Diagrams and linear-difference equation models, which act as calculators in the sense of "what goes in can be logically traced to what comes out".
3. The third archetype views the world as made up of feedback loops, such that cause and effect chains loop back upon themselves.
   • This is the view held by cyberneticists and by advocates of non-linear dynamics and chaos.
   • This viewpoint proposes that the world is largely chaotic and that you can no more predict the future from the past than you can predict next month's weather from last month's.
   • System thinkers in this domain use Causal Loop Models (CLMs) and non-linear difference equation models. Often their models behave counter-intuitively, suggesting that the phenomenon they are thinking about may hold some surprises.

We will look at all three approaches, but will concentrate on the third approach, as it is by far the richest and most rewarding, if only because it blows away prejudice and misconception. The figure above shows a simple Causal Loop Model for population. Open arrowheads indicate that the items at the tail and the pointed end move in sympathy, e.g., if Births rise or fall, then Population rises or falls in sympathy — or, more precisely, causally. You read the figure, then, as "a rise in Births causes a rise in Population"

Of course, a rise in Deaths causes a drop in Population. This inverse relationship is indicated by the filled-in arrow head. The whole figure then forms two loops, the one on the left reinforcing or positive feedback, and the one on the right counteracting, or negative feedback — hence the + and — in each loop.

The pair of interacting causal loops can be used as a kernel, about which to develop a more extensive Causal Loop Model (CLM). As an example, see below:-

 

.

Note: this model above is not yet a complete systems model, as total space and total food supply are unqualified sources.

Using CLMs to Illustrate

Desmond Morris, the anthropologist and author, described in his book "The Naked Ape" the likely reasons why humans are devoid of hair on most of their bodies — unlike any other simian. The CLM above illustrates this theory. To read the CLM, start at the top, and follow the arrows. The picture is taken from my book, Putting Systems to Work, Wiley and Sons, Chichester.

General Approach

The general approach to analysing complex systems recognizes that much of the complication results from dynamic interactions between various parts. So, the approach has tended to adopt the following route:-

• Ignore physical structure
• Concentrate on process, to understand the way a system might work, the way systems might inter act
• Use simple differential equations of the form :-
  • dx/dt = kx..........................exponential
  • dx/dt = ax - bx^2...............sigmoid / logistic / S-Curve
• Interlink equations :-
  • dx/dt = k1.x - k2.x^2 - k3.y.......( e.g. x is a herbivore)
  • dy/dt = k4.y - k5.y^2 + k6.x......( e.g. y is a predator)
• Such sets of equations are known as Lanchester equations. They can be used to explore complex interrelationships / competition / conflict

Computers solve such equations numerically

Towards Numerical Analysis

Eine Kleine Math Musik:-

• dx/dt = f(x)
• [x(n+1) - x(n)] / dt = f(x(n)
• x(n+1) = dt.f(x(n)) + x(n)..............a simple recursion equation
• In words :-
  • "New Level = Previous Level + Small Change Occurring During Short Interval"
• We may thus construct complex, dynamic models using simple building blocks of :-
  • Rates and Levels

Modelling Tools - iThink™ / Stella™

There are many modelling tools on the market which can be used to support rigorous system thinking. Personally, I tend to use Stella™. Some of its features are shown below:

• Reservoirs store things
• Queues accumulate things waiting to enter Ovens or conveyers
• Ovens fill with things and "cook" them for a period, discharging all together
• Conveyers carry things for the same amount of time, first in first out
• Circles represent flow rates, except after an Oven (Cook Time) or Conveyer (Time to Traverse)

Very many dynamic situations can be represented by these analogues. For instance, you could do your accounting this way...

The upper figure shows a flow (Income) entering a reservoir (Cash). The green line on the graph shows that the income is steady. The blue line shows the steadily increasing bank balance.

The lower figure shows a more realistic situation. The Bank, at left, makes monthly Payments in arrears into the Account. Outgoings comprise two parts:-

1. Fixed expenses (rent, utilities, etc.)
2. Outgoings dependent on the amount in the Account, e.g. you might spend more on parties and clubbing if you had more to spare

The resulting graph shows the money coming into the Account, in arrears, the Account rising at the end of each month up to a total of 12 months and then a fall — we lost our new job, didn't we! This is an example of linear, cause-and-effect, thinking. Useful, could be done on a spread sheet.

Queuing Models

Using STELLA™ you can address discrete problems, such as queues in which only complete integer values arise. Unlike the Account, where you can have part of a pound or dollar, in most queues you can have only whole values — e.g.whole people. The model shows items arriving in a queue at random intervals (Poisson), then being served and finally exiting. The model could represent a single supermarket checkout, for instance.

Note that the model is not yet a complete systems model, i.e., not the model of a whole system. This is evident by virtue of the "clouds" at source and sink, which imply an infinite population of arrivals, and an infinite sink for people exiting the queue. This model, then, explores a phenomenon, which may occur as part of a system. In a full systems model, the sink and the source would have to be, somehow, connected. Were this a model of a supermarket queue, then, perhaps, there would be several such models running in parallel, and an external population of people who shop in the area? Customers would be drawn from this population and would return to it after shopping. The variations in population would affect the queue lengths, and disaffection with excessive queuing would result in people choosing to shop elsewhere. Thus the full systems model starts to become more complex, non-linear and more realistic.

It is a defining characteristic of a full system model that it has no undefined sources and sinks, and no fixed external references — such as mean arrival rate in the example above. Paradoxically, then, the defining characteristic of a full systems model is that it presents as a "closed-loop" model. For this reason, if no other, it is useful to develop causal loop models (CLMs) of problems, situations and phenomena, prior to modelling them in STELLA™.

Thinking about Market Systems Engineering

All the above problems have been fairly linear, i.e., no feedback. This example takes us on into that world of non-linear, often counter-intuitive, behaviour and this is often referred to as Behaviour Modelling

The diagram shows products emerging from a manufacturer at left, becoming used and finally being perceived as obsolescent, or past their usefulness. The manufacturer is continuously improving the quality of his products, and as a result they becomes more reliable and contain less defects. He uses profits to fund more manufacture and he also uses some profits to innovate new products, so as to persuade customers that their existing products, although still working, are out-dated, outmoded, etc.

This is essentially quite a complex issue, and as the CLM shows, there is plenty of feedback, some positive, some negative. In talking your way around the model, it would be easy to confuse the various influences, so let's model it in STELLA™.

Comparing the diagram with the model, you will see how the one has been transformed into the other. Now to the results from running the STELLA™ model:-

The graph of Profit against Quality above might surprise you. It shows that 100% quality results in a significant loss of Profit. In fact, profit-growth is fastest initially for the 70% quality line, although it soon loses out to higher quality levels.

What is this all about? Well, this is a typical counter-intuitive response from a complex situation. Ultimate quality (100%) has two implications:-

1. It costs to implement
2. It destroys resales.

Why does it destroy resales? Well, I used to wear nylon shirts because they were easy to wash and never wore out. I can't buy any now. Why not? The manufacturer never got any resales, because his shirts never wore out, so he went out of business — at least on that product line.

If a model produces counter-intuitive results, you have to explain them!

The diagram also showed Innovation at work. This graph shows the effects of simultaneously:-

1. Increasing Innovation
2. Increasing Quality

We have seen the effects of increasing quality. Increasing Innovation should induce the buyer to buy more sooner, but innovation reduces profit, since it involves Research and Development, trials, etc. Putting the two together, as the graph above indicates, shows that there is an optimum — the purple line — in terms of profit, and that going either below or above that paired value will result in loss of profit.

Notice the graph axes have no numbers on them. These particular models are examining Behaviour, and we are interested in the general shape of the graphs, rather than in hard numbers — that might come later.

Toyota Assembly Line

Now we'll look at car assembly - Toyota are World leaders, and the following models show some of their now-classic approaches. First the assembly line.

In typical mass production factories, cars pass by workers on an assembly line. The flow is inexorable. Unless they are real show stoppers, snags, defects or problems tend to be tagged, so that they may be fixed at the end of the assembly line — so-called Post Assembly Repair.

Toyota, in the form of one Taiichi Ohno, developed a different approach to car assembly based on a simple, powerful idea. Instead of snagging defects, he stopped the whole line and teams descended on the snag to find it, pursue it to its origin, and root it out. Opponents of this new idea scoffed, suggesting that he would never get a car off the end of assembly. And, to begin with, it seemed they might be right. At each assembly stage snags occurred, the whole line was stopped, and problems were tackled

Gradually, however, Ohno's assembly line got better, until cars eventually made it all the way through to the end. These cars were virtually fault free — no Post Assembly Repair was needed.

The model above represents only one stage in an assembly process of many such stages. It shows good parts and bad parts arriving into the same queue for assembly. Bad parts are detected and diverted downwards, and operations held up while the bad parts are dealt with at source.

Kaizen at Toyota

This continuous process of improvement is called Kaizen. Kaizen is a philosophy. The mass production view of the assembly line is that you try to make it as good as you can from the outset. The Kaizen view is also that you try to make the line as good as possible at the outset, but that you recognize that you can never be perfect first time, and that there is always room for improvement. By continually improving, you must eventually approach perfection.

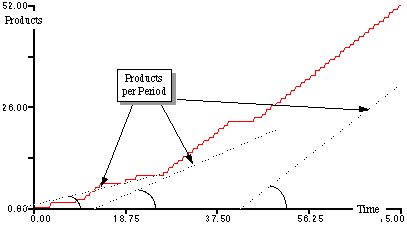
Kaizen at Toyota reveals itself in the distinctive, slow build to maximum output characteristic of Japanese assembly lines. As the graph shows, there are long periods initially where output is halted, but gradually these become less frequent until finally they virtually disappear

Systems Engineering Cost Models

Another subject area where counter-intuitive results may emerge is in Systems Engineering (SE). The model shows a simplified SE process, from Requirements at left to Commissioning at right. Requirements result in Design and hence specification of all the various parts that will eventually come together to form the deliverable product or system. Sometimes - generally — requirements contain errors, omissions, incompatibilities, etc. It takes time to correct these, and sometimes some of them get through into Specification.

These implicit errors then emerge downstream, either during development, or more likely during Integration and Test. The model shows feedback from these reservoirs to Design. This feedback is called rework.

The model explores the relationships between overall project costs and durations on the one hand, and the degree to which error eradication is effective at the start.

SE Cost Graph

The graph show commissioning effort (i.e., the end of the project) over time for various levels of Initial Error Detection. The results are staggering:-

1. At 100% (green line 4), the project terminates rapidly
2. At 70% and 80%, it does not terminate!
3. Notice that, near the origin, the green 100% line takes longer to start its climb, due to the additional time being spent on getting the requirement correct.
4. Notice also that 100% error eradication implies a high peak of commissioning manpower, since the shorter time scale means concentrated effort.

Of course, 100% error free requirements are a dream. But that's the point of system thinking. By seeing what the ideal can do for us, we can seek ways to reach towards that ideal — like Taiichi Ohno

The Three Body Problem and Chaos

One of the classic problems in physics is the three-body problem. Here it is in STELLA™, where three objects are represented by three coupled reservoirs. The graph shows the effect of increasing the coupling — an unexpected transition from periodic to chaotic behaviour. A simple model, but it produces complex behaviour. How many systems about us can, and do, produce complex, chaotic behaviour all the time, or could be on the edge of it and could be easily pushed over?

So, there we are — an introduction to a subject that I find utterly fascinating - I hope you found it at least interesting

Top of Page

Last updated: Jan 2005

hhttp://www.hitchins.net