Systems World

Contents

Chapter 1. Introducing Complexity

Chapter 2. Variety

Chapter 3. Connectivity

Chapter 4. Disorder

Chapter 1

Introducing Complexity

All theory, dear friend, is grey, but the golden tree of actual life springs ever green.

Johann Wolfgang von Goethe, 1749-1832

Questions of Complexity

What is complexity? Is it a commodity? What is it made from? How can it be measured? How does it arise? How does complexity relate to order? Can order arise from chaos? How does chaos relate to stability and complexity?

These questions, and many others, are the substance of this book, together with one other which is illustrated by Figure 1. The figure is taken from Horemheb’s scrolls, to be found in his tomb in the Valley of the Kings, Luxor, Egypt. (We shall meet more from Ancient Egypt later - their highly-developed culture affords non-sensitive information, much of it relevant to today’s societies). If you have not met such scrolls before, if you do not read hieroglyphics, and if you know nothing about Horemheb, then the scrolls will probably seem complex.

On the other hand, you may know that the duck signifies "son of" and that, next to the solar disc, they signify together "son of Re, the Sun-god". The eye and the two symbols beneath it, one of sedge grass and the other of a chair, signify Lord Osiris. Similarly, the left-hand cartouche indicates (approximately) "Amun loves Horemheb". This supposed devotion by the god Amun becomes more poignant when it is known that Horemheb seized the throne, rather than inherited by divine right, and had to assert his dubious god-given status.

Figure 1. Horemheb’s Scrolls from the Valley of the Kings, Luxor, Egypt

The scrolls rapidly lose their seeming complexity as one learns the meaning and significance of their parts - that is the point. The complexity is perceived rather than real. As we shall see, complexity can be real, too. After all, is complexity any less real simply because it is (only?) perceived?

Bak & Chen’s Self-organized Criticality

Bak and Chen researched into tectonic plate movement, seeking some pattern to earthquakes which might enable prediction. They examined models of sand dropping on to a disc mounted on a sensitive weighing machine. The grains of sand were chosen to be of similar size. As they dropped, a cone formed and grew to a critical size, above which there were slippages and below which there was a recurring build-up. Because the grains were of a size, it was possible to calculate the number of grains falling off the disc at each slippage, and a graph could then be drawn of the frequency of slips vs. the number of grains per slip. Not surprisingly, there were fewer "big" slips, with lots of grains, and more small slips with fewer grains. However, Bak and Chen also discovered that by plotting the frequency of slips of a certain number of sand grains on logarithmic scales, the data formed a straight line. The researchers refer to the phenomenon as "self-organized" because, as the cone grows above a critical size, it slips back and then grows to the same size. So long as the grains continue to fall, so long will the cone self-organize.

Bak and Chen described the relationship between frequency and numbers as "weak chaos", because it followed a power law relationship. (Chaos follows an exponential relationship). They and other researchers found that straight lines arose from other data, although the slope and start points would be different. Weak chaos has been observed in types of electronic (1/f) noise, stock exchange prices, distances between cars, deaths in war, and many more.

The Bak and Chen model is simple. Unlike many models, it is not built up from detail. One might, for instance model a sand cone by examining the characteristics of each sand grain, their angularity, coefficient of friction, stickiness, etc., and then model the way the individual grains fit together into a cone; this would be a micro model. Bak and Chen’s model is a macro, or system, model; it offers description of phenomena without resorting to a build-up of complex interaction detail.

Why do so many different phenomena produce straight-line curves when plotted as above? Is there some underlying behavioural similarity between them which we have yet to uncover? What links the distances between cars on a motor way, stock exchange prices and deaths in war? Perhaps the clue comes from electronic noise in resistors. One noise model proposes a vibrating ionic lattice with electrons tumbling through the spaces, getting snagged behind ions, and forming miniature piles of electrons which then slip in groups, resulting in the familiar spectrum of noise. The key may be in the progressive build-up and subsequent slip process, as opposed to random phenomena which, by definition owe nothing to previous events.

Complexity, Science and Engineering

Research is revealing that complex, interacting systems can develop organized behaviour (Ruthen, 1993). Biologists, economists and physicists have been observing that complex, open, interacting systems evolve toward a boundary between order and randomness. The subject which combines the interests of such diverse sciences is non-linear dynamics, and computer models of such systems can exhibit bizarre behaviour so that words such as chaos, anti-chaos, fractal and strange attractor have entered into everyday usage.

Conventional science and engineering have some difficulty with this macro/open-system behaviour. Engineers seek to control, to create order, to address linear problems where their mathematics can work. When their created systems interact with a complex world, results may prove counter-intuitive. Understanding complex system behaviour is essential to improve both scientific and engineering performance, but these notions have made little impact on many pragmatic (and successful) engineers.

Some complex systems seem very robust compared with their "engineered" counterparts and far-sighted engineers ask questions. For example, planned economies seem to be very sensible. They plan ahead, set reasonable targets, provide contingencies against risks or disasters, develop alternative sources and markets, yet they do not seem to survive. The evidence clearly favours survival in a free market, where much of the control is taken away, where competition is encouraged, where co-ordination between the various parts is minimized, where the law of the economic jungle applies. These are the very conditions industry and its engineers seek to avoid within their own organizations and designs, in the name of increased efficiency, effectiveness and quality.

Engineers in aerospace, particularly, have recognized complexity as an issue. Systems, they say, are inexorably becoming more complex to meet ever-more demanding customers; the task of engineering is seen as managing that increasing complexity. Is complexity the fault of customers’ demands? Come to that, is complexity "good", "bad", or immaterial?

Components of Complexity?

We know, from everyday experiences, when something is complex. A tangled jumble of wool is more complex than a neat ball. Snooker and pool are more complex than billiards, because of the various colours and their individual scores. A Formula 1 racing car engine is more complex than a Model T Ford engine because of the greater variety of parts all doing their bit to improve performance. On the other hand, there is nothing more complex about twenty identical paving slabs than about ten; it is not the number of things alone that makes for complexity.

There seem to be three components of complexity: -

• Variety
• Connectedness
• Disorder

Something is more complex if there is greater variety amongst its components, if the number of connections between the components is greater rather than less, and if the variety and the connections are mixed and tangled-up, rather than orderly. Following topics will explore each of these components in turn.

Fractal 1. Stars

Chapter 2

Variety

Variety's the very spice of life, That gives it all its flavour

William Cowper 1731-1800

Variety is a major component of complexity. Variety can be viewed as a commodity, of which we can have more or less. For systems to be stable, they may need a minimum variety: to adapt, they may need useful variety. Excess variety may change the nature of system behaviour.

Generation of Variety

Looking to the natural world, we see that the profusion of species, plants and animals, or "speciation", is greater in more energetic systems. For example, bio-diversity is much greater in a rain forest than in cold tundra areas. Is it too great a leap to note that car variety, the profusion of car makes and models, is greater in New York, London or Tokyo than in Moscow? In each case, the common theme is the amount of energy available; in nature, energy may be measured in joules, while in economies it may be measured in wealth. We may note similarly that the variety of weapons in the respective arsenals of the US and the UK favours the US; not only does the US possess more weapons, but a greater variety of weapons

It is tempting to deduce that variety is somehow generated or "pumped" by energy, although we might have to be a little free in our interpretation of energy according to situation.

Energy, Source of Variety

It has long been established that species evolve to be efficient users of energy (Lotka, 1922). If two species compete for the same resource then, during times of shortage, the more efficient will survive. On the other hand, during times of plenty, when speciation occurs - as it does naturally owing to genetic inheritance from two parents - variety may be supported by the environment to propagate and evolve further. Subsequent reduction in available energy may see new species sufficiently changed to be able to shelter in new niches.

It is tempting to equate these ideas to recession and the rise of a variety of businesses during times of plenty, only to see many of them - but not all - go to the wall when times are harder.

Both the natural and the business worlds behave, in this respect, in a way which is consistent with observation of living on the "edge of chaos". To an observer standing somehow detached from the activity, species/businesses generate and multiply, then fall back again, filling the constantly-changing ecological/economic "space" in a seemingly haphazard manner. From this perspective, variety seems to come and go in a complex, continually-shifting pattern.

Variety

Addressing complexity as a subject allows that variety, connectedness and disorder may be treated as commodities, and this is so far outside of our usual experience that it can appear strange at first. For example, the concepts of "not enough", or "too much" variety are not easily grasped. In following topics, we will explore the following variations on variety: -

• Minimum Variety
• Useful Variety
• Limited Variety
• Excess Variety

Minimum Variety

The western world, with its many mouths to feed, has developed agriculture based on large scale monocultures. Western farmers grow vast fields of a single species of wheat, or farm salmon spawned in great quantities, or grow a single species of apple. Singular varieties are known to be susceptible to disease, or predation, and a complementary industry exists to provide artificial fertilizers, pesticides and a supply of new, disease-resistant varieties. Genetic engineering is coming to the aid of farmers who are finding that nature is rather good at generating diseases and predators to damage or feed off their mono-crops. The genetic engineers hope to keep ahead of the game by conferring disease resistance, say, from one species to another. The approach is necessary to support the enormous population, but it is also energy intensive.

Figure 2. Some component systems of the human/mammalian body. With the exception, perhaps, of the reproductive system, none of the component systems could be removed and leave a viable body

South American farmers have farmed using polycultures for many hundreds of years: polycultures bring together complementary plant varieties - mutual nitrogen fixation, natural pesticides/herbicides, wind-brakes, climbing frames, etc. The different plants, working as a set, combat a wide range of threats/potential deficiencies. In the western world, these techniques are well known to domestic gardeners, too, with marigolds and cabbages (for instance) being planted together, since the marigold protects against some cabbage pests. Polycultures require much less energy in the form of artificial aids. Their disadvantage, of course, is the unsuitability for mechanisation which militates against large scale cultivation.

Polyculture farmers probably identified suitable combinations of plant variety by trial and error in the first instance, which raises an interesting question - how much variety is enough? Clearly there could be inappropriate variety, but can there be too little, or too much, as well?

As Figure 2 shows, the various systems within our bodies are complementary, or mutually supportive. With the exception of the reproductive system, little could be removed without serious and immediate death. Even the reproductive system would not be removable if the term "viable" were taken to include self-reproducing. (Non-essentials such as appendix and gall bladder have been excluded; for most adults, they are not essentials for viability.)

As Figure 3 shows, the viability of any system is determined, not only by the internal complementary parts, but also the threats which it has to meet. The greater the environmental diversity or threat, the greater the minimum variety essential to viability. This idea suggests that there may be a potential mathematical basis for determining minimum variety, based on cause and effect.

Useful Variety

The concept of useful variety is distinct from that of minimum variety. Useful variety makes essential, complementary contribution. For example, the variety of clothes and sizes in clothes shops makes a useful contribution to the ability of the shop to satisfy its varied customers. Beyond the smallest and largest likely clothing sizes, variety would not be useful. Alternatively, consider a word processor or drawing program with varied capabilities for varied people, tasks and environments. Beyond some limit, more variety in the capabilities of the program is superfluous, and could make the program difficult to understand and to use.

Determining the sensible limit of usefulness may not be straightforward. In the clothing shop example, it might be possible to analyse the likely population and to stock only sizes that would sell, although the existence of outsize, short and tall specialist shops testifies to the difficulties of meeting this goal. On the other hand, the ideal variety of capabilities in a word processing package depend upon the tasks it will need to face after purchase, and these may not be so easily predicted. Or, how about the skills that a company should retain during recession to enable rapid start-up once the recession lifts? Holding redundant skills against a future need is tantamount to predicting the future which, in the event, may not be knowable.

Useful variety, then, is less amenable than minimum variety to mathematical determination, since it implies prediction. Nevertheless, we often choose in everyday practice to hold on to something, or to buy a product with variety which we may not need directly, as a hedge against the uncertain. Useful variety is part of risk management.

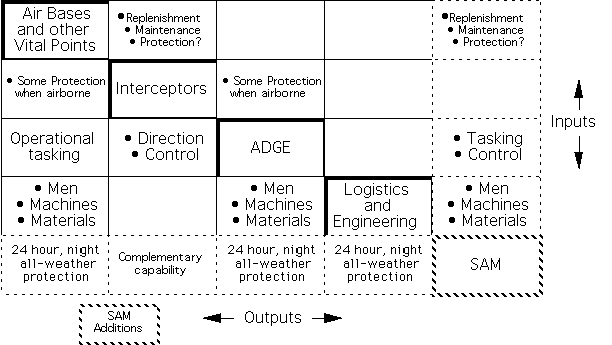
Figure 3. An N-squared chart showing a typical air defence organization. In an N-squared chart, component systems are shown on the leading diagonal, with the other rectangles representing interfaces/relationships/interflows between the systems. So, Interceptors give "some protection when airborne" to both the Air Defence Ground Environment (ADGE, or ground radar and command network) and to the Air Bases and other Vital Points. The bottom right rectangle, representing Surface to Air Missiles, is cross-hatched to show that it is needed only if the airborne threat to the other members is significant. Were a tactical ballistic missile to be considered a threat, then an anti-missile missile would be needed in addition to SAM. The minimum system variety to ensure viability is partly determined by the external threats to the system.

Limited Variety

Limits to variety can be both perceived and real; first, perceptions. If one asks how many great religions there are, the answer seems to come out at "rather less than a dozen". Judao-Christianity, Islam, Confucianism, Buddhism...before long we start to struggle. If we consider, say, Christianity alone and ask the same question, Catholicism, Orthodoxy (Russian and Greek) and Protestantism emerge...and we start to falter again. Keeping going, if we look at the Protestant sects, we find Methodists, Baptists, Calvinists, Lutherans, and so on; again, we soon start to run out.

The phenomenon is not confined to religions. How about ethnic groups? Negro, Mongolian, Semitic, Caucasian, Aborigine, Indian...we soon slow down. If we take any one, it can be broken down into a relatively few divisions. As we increase the resolution, we seem to see the same broad constraint on variety emerging, no matter what the general topic. Why should there be a limit? Why is it so small?

Psychologists and anthropologists propose that there is some in-built, simian inheritance in our brains which tends to make us confused when we try to contain more than about seven mental categories at the same time. (See Miller, 1956.) Experiments with dots randomly scattered on a sheet of paper, and shown for only half a second or so, suggest that perception of numbers of dots up to about seven is simple for most people. Beyond seven, there is a sharp cut-off, with most people responding with "lots of dots".

Could it be that our reaction to things or situations as being complex is nothing more nor less than an inherited mental processing limit? Perhaps during our evolution, it was unnecessary to address more than seven or eight categories of anything at the same time in a life-threatening situation; perhaps we evolved an ability to perceive up to seven things in parallel under "fight or flight" conditions. If "Miller’s seven" (as the phenomenon is called) is simply that, a subjective and inherited limit of human parallel processing, then perhaps complexity itself is simply our mental processor balking when we try to process too much variety at once…

There are real limits to variety also; these will be explored in a later topic, and are concerned with the relationship between the energy entering an open system, and the resultant speciation.

Fractal 2. Level Cross-roads

Chapter 3

Connectivity

Ah, but a man's reach should exceed his grasp, or what's a Heaven for?

Robert Browning 1812-1889

About Connections

Open systems can be viewed usefully from a functional viewpoint as receiving inflows (of substance, energy/power and/or information) transforming those inflows into different outflows and passing them on to other open systems. In the process, open systems absorb sustenance from whatever passes through them. Humans are open systems, and we operate in just this manner. So too do organizations, social groups and processing plants.

From this system viewpoint, connections appear as enabling, supporting or directing flow between open systems, much as veins and arteries enable the flow of life-giving blood. Bundles of connections can be grouped to reduce perceived complexity.

Bundles of links can be viewed as systems, too, but there is a distinct difference: connection bundles do not materially transform whatever flows through them. See Connection Strategies later.

This differentiation into transforming and non-transforming systems is useful in reducing perceived complexity. We can also identify types of connection; these may be two-way (duplex), or one-way (simplex). Telephone lines carry speech in both directions, and are duplex. Power cables support uni-directional current flow and are simplex. The distinction between simplex and duplex is useful. One-way connections permit asymmetry, introduce notion of reachability...

Reachability

Fig 4. Reachability. Five entities, A to E can be connected using either duplex (two-way) links at left, or simplex (one-way) links at right. The right hand structure is asymmetric, D and E cannot reach each other, neither can A and B.

As Figure 4 shows, duplex connections favour symmetric relations, while simplex connections favour asymmetric relationships. In the figure, reachability is an issue. For example, is A reachable from B? In the left hand picture, A would be reachable from B if, and only if, C enabled the connection. C would be described as transitive. If C were transitive in the right hand diagram of Figure 4, D could reach A and B through C, but could not reach E (because of the simplex link from E to C); D and E could not be reached at all, and A and B could not reach anything. If C were transitive in the left hand diagram, there would be complete reachability.

Transitivity

Figure 5 shows the impact that transitivity can have on perceived complexity. At the left, all connections are shown between boxes, presumed non-transitive. At the right, simply by assuming transitive boxes and suppressing redundant lines, the perceived complexity is greatly reduced. A physical realization of the two figures might find the boxes in the left diagram having a number of different communication links to other boxes, while at right each box above the lowest pair provides a through-communication service. Note that the real complexity is still as at left - nothing has changed logically.

Figures 4 and 5 are typical of the representations we employ to convey ideas. Figure 4 might represent some system or organization. Figure 5 might be a "tree" of objectives which contribute to each other via the arrows. (For a practical example of such a tree, see Figure 29.)

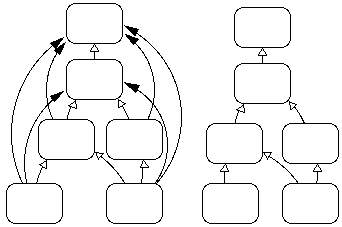
Figure 5. Transitivity. In the left hand tree diagram, boxes are assumed non-transitive, and all simplex connections are shown. In the right hand diagram, all boxes are transitive and redundant connections are suppressed.

Complex Behaviour

Observance of chaotic behaviour in the real world has shown that it can develop from the simplest of (seemingly) well-behaved parts. Complex behaviour demands very little variety, but it does require, inter alia, connection between parts and non-linear behaviour of those parts. It seems that strength of connection can affect behaviour.

Consider just three bodies (e.g. quarks, suns, etc.); their interaction pattern should be simple enough to predict; after all, they must obey the laws of physics. As Figure 6 illustrates, three elementary interacting bodies may behave in an orderly, chaotic or unstable manner according to the strength of coupling between them. At left is the simple view of three interacting bodies. Interactions between the bodies is two-way, to a strength determined by the "amounts of stuff" in each of the connected systems; and coupling between them. Conditions are identical for all three systems in the model. The graph, at right, is the result of a computer simulation of the systems, and shows the "stuff" an any one of them. In the graph, only the coupling is changed, in the middle. The left hand section of the graph, low coupling, is well behaved, although the non-sinusoidal shape of the wave might suggest some non-linearity. The right hand section of the graph, high coupling, behaves erratically.

Physical realization of the conditions used to model the three-body problem are not hard to visualize. For example, the gravitational attraction between two bodies is given by the well-known relationship: -

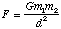
where:

F = Force

G is the universal gravitational constant

m 1 is the mass of body 1

m 2 is the mass of body 2

d is the distance between the two bodies

For three bodies, the mathematics is similar, giving results similar to those in the graph.

Figure 6. Three Body Behaviour. Three bodies move under mutual attraction, at left. According to the degree of their mutual inter-coupling, their behaviour may be periodic or chaotic, at right. If three simple hard bodies can behave in this fashion, how might three complex soft bodies (people) behave?

If such complex behaviour can result when three simple interacting bodies are closely coupled, what might the be complexity of behaviour for three soft bodies, (e.g. humans, interacting ecologies, etc.). Would their interaction pattern be more, or less, complex?

Bounded, Stable Chaos

Figure 7. Hénon chaos. The pattern shows the interaction of simple differential equations as a coupling factor between them is increased.

Chaotic behaviour may be complex, but it is not random. In Figure 7 there is a map of Hénon Chaos. The map is built up from simple, non-linear equations. As a coupling factor is increased, the pattern starts from the centre and moves out, producing, initially, concentric "circles"; for each increase, there follows a greater radius. Each "circle" is built up from individual dots, which develop the locus in an orderly fashion.

As the coupling factor increases further, behaviour changes, until the five ovoid shapes emerge, within which there are no dots. No matter what the coupling factor, no dots can appear in those ovoids. Still further increases seem to revert to a more concentric pattern until the equations finally go unstable - witness the dots at the edge of the picture frame.

Connection Strategies

Figure 3 presented an N-squared (N2) chart, which is useful in simplifying the complexity of connections. For example, an N2 chart has N x N squares, N of these are on the leading diagonal where they represent the parts of the system, leaving N2 minus N squares to represent all possible interfaces. So, we can do some simple sums: -

Maximum number of simplex links between N entities = N2 - N

If N = 5, then the maximum number of links = 20,

If N = 20, then the maximum number of links = 380

In quadrupling the number of entities (from 5 to 20) the maximum number of links rises (from 20 to 380, or) nineteen times. This is close to, but slightly greater than, a square law.

As the parts in systems become more numerous, the potential for interconnection rises rapidly. Systems with many connections may spend much of their time and effort on receiving inflows and sending outflows. In other words, it is possible for an entity to become "over-connected." Over-connected entities spend more energy processing interchanges than transforming inflows to outflows.

Observing the world around us, there seem to be some four archetypal strategies for addressing this issue of over-connectedness: -

• specialized interconnector-systems. Some systems become specialized connectors e.g. railways, telecommunications, nerve cells. In essence, they cease to transform inflows to outflows, acting instead as transporters. Railways transport people without materially changing their state. Telecommunications and nerve cells transport data without materially altering the message they represent
• interconnection strategies to avoid full connection. Some systems employ strategies which result in connection via convenient, but indirect routings. Telephone connections between individuals in different cities cannot be direct - there are simply too few wires. Instead, telephone calls are passed through exchanges where, using a number of strategies, many calls may be sent down a single connector between exchanges, subsequently being separated out for onward connection. The strategies include time, frequency and code multiplexing, all designed to overcome the capacity-limits of discrete connectors
• stay in small sets. The problem of over-connectedness does not arise if entities stay in small sets. We humans socialize in small sets, as any cocktail party will suggest. As more people arrive, they progressively break into relatively small groups so that the individuals can converse with relatively few friends at a time. Individuals may then migrate between groups from time to time, which can lead to...
• stochastic/chaotic connections. Sometimes entities need to communicate across a broad front, but cannot afford the overhead of continuous, full connectivity to all potential communicants. They may then adopt a strategy of full communication but for only part of the time. This strategy may be organized or disorganized. Managers at work would prefer, sometimes, that it were organized and hold meetings accordingly. However, the unpredictability of business requires discussion and decision-making "on-the-fly", and connection patterns between managers and workers may become chaotic. In this context, the term chaotic need not be pejorative; chaotic interaction may be necessary for successful overall system operation

Connection Symmetry and Simplicity

Figure 8 represents a not-untypical connection strategy amongst entities - the "nearest neighbour" strategy connects each entity to its nearest neighbours only. The strategy is not remarkable, but the consequent number of links presents interesting features according to whether or not the entities are grouped symmetrically, as follows: -

• 16 entities in a single cluster, fully connected = 240 connections
• 16 entities in 2 clusters of 8 employs 114 connections
• 16 entities in 2 clusters of 6 and 2 clusters of 2 employs 76 connections
• 16 entities in 8 clusters of 2 employs 72 connections
• 16 entities in 4 clusters of 4 employs 60 connections

Figure 8. Sixteen entities arranged into four groups of four in a flat connection structure (i.e. two-dimensional). Diagram can also be interpreted as a simple hierarchy with the single central figure omitted. The diagram represents a "nearest neighbour" connection strategy.

The numbers suggest that there may be a connection infrastructure minimum at the point of symmetrical grouping of the entities.

Figure 9. The chart shows the number of connections needed to join a given number of entities, according to the number of clusters into which the entities are grouped. The front set of columns corresponds to Figure 8, with sixteen entities. The rear set of columns corresponds to 32 entities. Note that the minimum is sharper as the number of entities increases. Note, too, the discontinuous X-axis

Figure 9 employs the same connection strategy as Figure 8. Note that minima sharpness, i.e. potential infrastructure reduction increases with the number of entities to be dealt with. For many inter-connection schemes, there is a grouping strategy which minimizes infra-structure.

Natural systems may evolve towards such minima where there is survival advantage, e.g. less energy absorbed in the interaction. This potential survival advantage may explain some natural symmetry such as, for instance, the tendency of migrating birds to fly in extended V-formation. It is believed that this formation reduces the energy expended by the flock overall.

Cocktail parties seem to evolve into similarly sized groups to reduce overall hubbub, enable easier discussion in group. At the start of a party, a single group forms, but splits as further guests arrive. The reasons for the split may be several: circle becomes too large for conversation across the diameter; larger circle exceeds Miller’s seven; too many cross-conversations are possible, and their mutual interference causes the group to fragment; etc. In any event, it is noteworthy that as more guests arrive, groups form and reform until the room may become filled with many similarly-sized groups, all talking at each other. Members within a group will close up to hear others speak above the general hubbub. Systematically, the overall party self-organizes into symmetrical groups, so reducing the total number of simultaneous person-to-person interactions, and hence the overall noise - or, alternatively, increasing the number of simultaneous, successful conversations. At its height, a cocktail party can seem so complex that it appears to be total chaos - but perhaps this is just our perception.

For many inter-connection schemes, there is a grouping strategy which minimizes infra-structure. Organization designers generally ignore such factors, however; we tend to see the trees, rather than the wood. Looking at the cocktail party, it is easier to see one or two groups, less simple to see the whole party as one system.

Connections and Control

Within both management and engineering, connections between and within systems are used to enable control. Figure 10 shows the scheme from a management viewpoint. A manager has a desire to change or regulate something. They perceive some divergence between that which is, and that which they wish. The difference is used to generate a correction instruction/plan, the plan is implemented and some convergence occurs which reduces the deviation. In control engineering, the scheme is essentially similar, but more precisely regulated in terms of the dynamic response of the item being regulated.

Figure 10. A simple model of management through control

As the figure illustrates, control is essentially negative feedback, minimizing deviation from some desired target. Control in management seeks co-ordinated response among subordinates to achieve a manager’s desire. This simple notion conceals some less obvious issues: -

• Control in management seeks co-ordinated response among subordinates to achieve manager’s target
• Control, therefore, tends to encourage the ideas and initiatives of only one person - the manager.
• Control limits subordinates. A manager may have many subordinates, many of whom may know the details and practices of the work in hand rather better than the manager. Control inhibits the subordinates by determining what they can and cannot do.
• Control demotivates subordinates, by the process of inhibiting them.

Figure 11. The Puppet Hierarchy

Figure 11 explores the idea of management control further. It is based on observation of a French ventriloquist, who had a dummy which, in its turn, had another dummy. The larger dummy was teaching the smaller dummy to be a ventriloquist...

In the figure, which represents some views of authoritarian management, the upper puppet controls the lowest puppets through the intermediates by pulling appropriate strings. Clearly, this is not simple. For a start, control requires feedback, up the strings, and the top puppet must be able to sense the response from the bottom. Add to that the idea that management "strings" are made from "soggy elastic" leading to connection delays, and allowing for puppet inertia and we may agree that management control is not practicable using this model. So, how does control work?

Control in Action

Evidently, control must mean something quite different in practice. Figure 12 shows an alternative view which seems more tenable. A director (someone who directs, rather than a necessarily-senior person) gives a "doer" bare instructions, based on the directors mental model of the situation and the task in hand. The doer interprets these bare instructions and expands them to meet the needs of the occasion, using his or her mental model. The doer’s actions result in some change or event, which may become evident to the director, who thus sees the consequences of the original bare instruction.

Clearly, this is not the same sort of control as the puppet concept. There are several important differences: -

• The director’s and doer’s mental models may differ. The director may have dated knowledge of the task to be undertaken by the doer: they may have different objectives
• Feedback may occur some considerable time after the instruction. Should the director re-direct in consequence, the situation could become unstable, with instructions to change arriving with the doer after he or she has already changed.

In many circumstances, however, Figure 12 seems to be a more likely model of management control than Figure 11. Management control contains within it, then, the potential for highly complex behaviour as individual directors issue instructions to a multiplicity of intermediates, who in turn pass on the instructions to the eventual doers. At each stage of this "Kim’s Game" there may be expansions of the bare instructions, mistakes in repetition and interpretations based on non-aligned mental models.

Figure 12. Control in Management

Connections and Synergy

The term synergy is used in different ways. In the present context it is defined as: co-ordination and co-operation between parts within a system to produce some desired external effect. Instead of the vertical hierarchy of Figure 11, synergy evokes a flat team structure for management, Figure 13. The figure represents seven meshed teams, six around the periphery and the seventh in the centre. Each peripheral team has a team leader (T) who is a worker, too. The team leaders also operate within a team with a co-ordinator (C) who facilitates interaction between the teams, co-ordinating their mutual interactions.

The figure presents a flat team structure. Unlike the vertical hierarchy, it encourages participation within teams and competition between teams. If it can be made to work, then the result is creative synergy - provided all share same target. How this shared target might come about will be examined below.

Figure 13. Flat management. T - team leader C - co-ordinator

Synergy

One view of the mental attitudes of people in an organization is given in Figure 14. At the left, people are seen as having different, uncoordinated viewpoints, represented by map compasses in the absence of an external magnetic field. The arrows point in different directions and, although the individuals may be industrious, the net result may be disappointing.

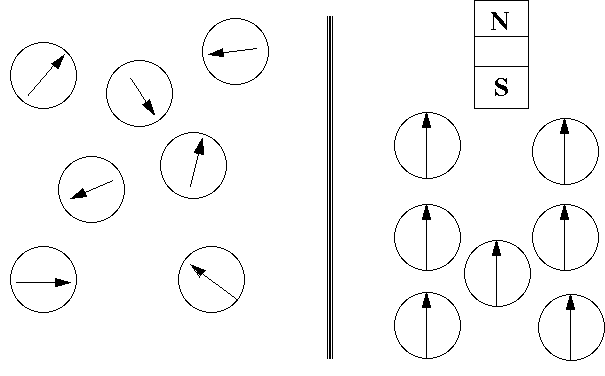
Figure 14. Goals and Synergy

On the right of the figure, the compass needles have become aligned owing to the introduction of a bar magnet which attracts them all in the same direction. In management terms, the attractive influence might be some shared vision to which everyone subscribes. A control viewpoint might invoke discipline as the way to make everyone "point in the same direction". We might describe vision as "pull" and discipline as "push". In different situations, either or both might be appropriate. In either case, the result is some degree of synergy, reducing the complexity (variety) of group behaviour.

Synergy can emerge in other ways, and is observed in Nature. Trees have been observed to change their growth pattern when other trees are being over-grazed by antelope in Africa. The suggestion is that over-grazed trees emit some chemical messenger which stimulates those down-wind. The mimosa plant is also observed to wilt extensively when touched, although it does not appear to have a nervous system through which instructions, both to wilt and later to recover, might pass.

Synergy in the military is often achieved through the use of SOPs - standard operating procedures. SOPs are pre-agreed routines which are invoked either at a pre-determined time or on the occurrence of some event or situation. The key point is that no orders need be given at the time when the SOPs are activated. This obviates any need to communicate which might reveal presence or intent to an enemy.

Fractal 3. Connectivity

Chapter 4

Start

Disorder

A sweet disorder in the dress, kindles in clothes a wantonness:

A lawn about the shoulders thrown into a fine distraction.

A careless shoe-string in whose tie, I see a wild civility:

To more bewitch me than when Art is too precise in every part.

Delight in Disorder, Robert Herrick, 1591-1674

Entropy, Measure of Disorder

Variety and connectedness do not fully ‘capture’ complexity. In addition, orderliness is important, too. The concept is illustrated in Figure 15. The diagram at left seems less complex than that at right, although both have same entities, the same connectedness, and the same variety

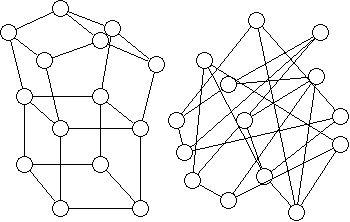
Figure 15. The two diagrams have the same numbers of nodes and links, but the figure at right seems more complex, simply because it is more tangled. The overall length of the links in the left-hand diagram is much less. If the nodes are free to move, and if there is some advantage in overall-reduction in link-lengths, then the figure at left may evolve from the figure at right.

Note that the figure at left has, in the course of reducing the overall link-lengths, become much more symmetrical - another way of expressing the reduction in tangling which has taken place.

Configuration Entropy

For tangible systems, entropy and energy have a defined relationship, albeit a very complex one in many situations, so there is a correspondence or equivalence between an approach based on entropy and one based on energy. Additionally, entropy allows the non-tangible to be considered. There are many definitions and views of entropy, some based on thermodynamics, some on the number of ways in which things can be arranged, i.e. stochastic. They are mathematically equivalent, but particular definitions suit particular purposes. In general, as is well recognized, entropy measures the degree of disorder in a system. Two types of molecule in a box full of two gases would generally be mixed; if work were done, each molecule type could be moved to different ends of the box. This less disordered, reduced-entropy state is achieved by doing work on the molecules, by expending energy.

Adding cold liquid creamer (rather than dairy cream) to hot coffee in a cup can result in most impressive and bizarre 3-D chaotic mixing patterns before eventually reaching a complete mix. Thermodynamic considerations show that the entropy of the mix is greater than the sum of the separate entropies of creamer and coffee, and common sense will tell us the same - the separate liquids were clearly in a more ordered state before the chaotic mixing. Adding the last piece to a jigsaw puzzle, on the other hand, completes the picture and reduces entropy. In this case, specific inter-relationships between parts are important, and the disorder is less when the jigsaw is intact. One view, then, of entropy is concerned with the way things are organized in relation to each other. This can be called configuration entropy.

Configuration entropy is the degree of disorder in pattern, organization and structure. Zero entropy is exemplified by a perfect crystal at zero degrees Kelvin: there is no movement, no vibration, bonds are regular, ordered and at their lowest net-energy state. Configuration entropy can be used as a measure of all kinds of disorder: heights of people in a queue (are they in height-order?); books on a shelf (are they ordered by colour, size, subject, frequency of use?); fields on a farm (are they equidistant from the farm, rectilinear or shaped, arranged to offer minimum tractor travel?); and so on. If we wish, we can calculate entropy quantitatively; it is concerned with the way things are arranged and with their relationships. However, the notion of configuration entropy may carry us further if we temporarily put aside the urge to calculate, and proceed with the concept qualitatively - knowing always that, in principle, we can calculate should it prove useful.

Consider a medieval countryside, perhaps in rural England. Human occupants enter the land, somewhat haphazardly. They associate into, say, three or four villages. The ‘coming together’ into villages represents a reduction in overall disorder, when compared with the previous meanderings. The three villages independently set up organizational structures: they elect leaders and allocate tasks to individuals, they till the land and raise cattle, seeking to create order. Disorder (entropy) seems to be reducing. Now, some of the villagers set out to explore, find the other villages and move home. In the process of leaving their villages and exploring, disorder increases. As they settle into their new homes and, perhaps, bring new organizational ideas and structures to bear, disorder again reduces. Perhaps there is a pattern in open systems, with disorder first increasing and then reducing, to be followed by another increase and then a further reduction.

In the same vein, it is possible to consider systems as, by their nature, reductions in entropy - at least within the boundary of the system. Similarly, connections between systems, bringing order and structure, must reduce configuration entropy, although entropy may well have increased during the creation of the links. At a fundamental level, it seems likely that the common thread binding all systems ideas together is the desire to perceive order, to reduce entropy either in fact, or in perception. Kast and Rosenzweig (1972) observe that open systems tend towards greater differentiation and states of higher order (reduced entropy). We see energy promoting entropy and systems forming to reduce it - hence, perhaps, the continual variation in entropy. For our purposes, since we are dealing with complex patterns, configuration entropy is the most suitable idea: -

Increasing energy increases entropy or disorder.

How Might Order develop naturally from Disorder?

There appear to be at least two concepts for the spontaneous emergence of order from disorder: -

• Since a complex system is made from many interacting parts, it might seem that there are a vast number of ways in which those interactions could occur. However, it is also likely that there are relatively few of this potential combinatorial explosion of possibilities which can self-sustain, i.e. produce a viable whole
• Some processes within, and interactions between, the parts of a complex set of systems may require less overall (lattice?) energy, conferring survival benefit on particular arrangements

Following topics explore these alternatives.

Viable Pattern Development

Figure 16. The progressive development of complementary systems to produce a self-sustaining set.

Figure 16, top matrix, shows five systems, initially unconnected, perhaps wandering freely and coming together by chance. They might represent some biological organisms, or perhaps organizations within an economy. System 1 is able to synthesize four discrete varieties, a, b, c, and d into four composite varieties. System 1 synthesizes these composite varieties, abc, bcd, cda and dab as a continuous process, and creates a local environment rich in the composites.

System 2 is able to decompose variety abc into a and bc as shown in the second matrix. Systems 3, 4 and 5 also decompose their composites as shown. The interchange of varieties between each system is now balanced, with each receiving the varieties it needs, and each providing the varieties needed by the others - so long as the external discrete varieties continue to enter System 1 from outside the set. You may check this by observing that the varieties entering each system (in its column) are the same as the varieties leaving that system (via its row).

The result is stable. Each System has its needs met, and has no need to expend energy in seeking an essential, but missing, input. Indeed, we can treat Systems 1 - 5 as a single item, e.g. System X. This is order emerging from disorder. The pattern is also particular - while there are several patterns of decomposition which would satisfy the conditions for the second matrix, many decompositions would not reconcile the column/row rule for variety in/variety out.

The patterns, once formed, also resist change. Figure 17 shows a slightly more complex arrangement of system interactions than those of Figure 16, with four discrete varieties, a to d

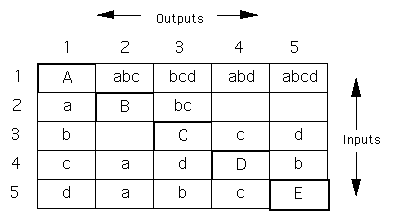
Figure 17. A synthesis/decomposition set used as a basis for the simulation of Figure 18

The matrix has been simulated to observe its dynamic behaviour, Figure 18. The simulation shows how tolerant of sudden changes in the external environment the set of interacting systems has become. Perturbations are rapidly smoothed out and shared between the five Systems, A - E. This resistance to external perturbation is open systems stability.

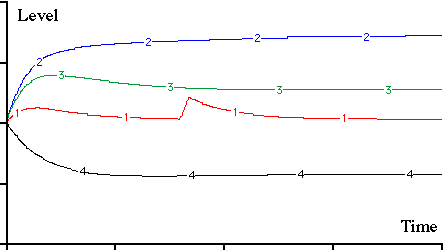
Figure 18. Dynamic simulation of the matrix of Figure 17, showing the levels of the four varieties within one of the systems. A large pulse of variety a (trace 1 on the graph) is introduced from an external source. Note how its effect is absorbed and distributed amongst the other levels.

Reducing Lattice Energy

Entropy, or at least a measure which is a useful, practical measure of disorder, underlies the technique at work in Figure 19, which is a useful way of developing the structure, organization or architecture of a complex arrangement of things. The things in question might be people at desks in an office, software modules in a processor memory, microbes in a soup, electronic components in a design - almost anything where a system develops disordered, connected variety.

Figure 19. The figure is read clockwise, starting with the top left diagram. It shows a tangled set of connected entities. These are mapped into the matrix, top right, which is evolved using a genetic algorithm to the more ordered matrix, bottom right. This, in turn, maps into the untangled set, centre left, which can be perceived as a higher level set of systems, bottom left.

The tangled set of interconnected entities in the figure is translated into the matrix, which is scored by the simple expedient of measuring the distance of each of the numbers, representing a connection, from the letters, representing the entities. Using a genetic algorithm - a program that evolves the answer - the lower matrix is evolved, in which all the letters are connected exactly as before, but the re-ordering of rows and columns has reduced the entropy. The pattern of "1s" looks neater and tidier, too. Mapping back into the systems domain results in the untangled set of systems at centre left, which is both visually and mathematically simpler and less complex. Finally, at bottom left, comes perception of order. Reducing the tangible disorder has enabled us to see higher order systems - this is a perception jump, it reduces disorder in the brain. An example of this process of lattice energy reduction, used in the conception of a complex system, is shown later - see Figure 40.

Feeling the Penny Drop

When we finally understand a complex situation, we experience a sense of completeness or satisfaction. Do our brains naturally search for reduced entropy? Is this search for reduced entropy behind: -

• right-brain activity
• dreaming
• déjà vu
• that essential part of a problem popping into the mind when doing something completely different?

Perhaps the brain evolved as a sophisticated reducer of perceived disorder, hence categorization, stereotyping etc., might be naturally-evolved means to reduce complexity (and duration) of mental processing. In fight or flight situations, it might be essential to survival to reduce mental disorder.

Consider the following simple problems which suggest how our brains seek states of reduced disorder. In attempting to solve the problems, try to observe yourself at work. You might find the following: -

• The sequence of letters can be completed only after the context in which the letters occurs has been identified
• First, search for context
• Second, invoke context-specific tacit knowledge
• Result, feeling of completeness, satisfaction (and a subsequent inability to unsee the solution!)

1)

_ _T W T F_

2)

       H

       A

  LA_ IER

       E

If you find difficulty in solving the first sequence, count how many letters there ought to be - that should provide sufficient context for the answer to appear, but where does it appear from?

If you have difficulty with the second sequence, did you try to complete the shorter, vertical word first, then see if the horizontal word fitted? Did you employ the strategy of going through the alphabet? Most of all, did you notice that feeling of simple satisfaction when you eventually solved the sequence?

Summary

There seem to be at least two ways in which order may emerge from disorder. Both means of developing order - Complementary Systems and Darwinian Evolution - occur in Nature, but each is quite different. Both means seem equally likely to occur with organizations as with organisms: -

• Complementary Systems can form rapidly, through chance encounter (or by design). Not restricted to biological forms. Very few of possible configurations actually complement each other - others may not complement, may even be mutually inimical. Group consumption of energy lower than sum of separate set members
• Darwinian evolution essentially biological, takes a long time, evolved species are most efficient users of available energy

Perhaps it is not quite as simple as the two bullets suggest, however. Evolved flora and fauna also form complementary sets - prey/predators, food chains, CO2/O2exchanges, etc. The natural world evolves systems which survive by forming into complementary sets, evolving again as their environment changes. Could these two features form the essential basis for the underlying stabilities of economies and social systems?

Fractal 4. Curls

Part 2 Getting a Handle on Complexity

Start

Last updated: Sep 2002

http://www.hitchins.net

P