Systems World

Application of the Systems Methodology
- Land Force 2020

Systems Methodology Step 6 - Design Optimization

Optimization results in the "best" solution to the problem, where best may be:

• Best value for money
• Lowest risk of Blue casualties
• Most cost effective
• Maximum ROCE
• And many more

Generally, optimization is about compromise

• E.g., most cost-effective is not the most effective It maximizes the ratio of effectiveness:cost, giving best value for money.
• Most effective may be unaffordable

Apollo compromise was about mass, volume, capability and risk between the various parts

Measuring the effectiveness of LF2020 - it has slipped a decade after looking at the technology - will be more difficult, but vital. (With hindsight, you might have seen that coming!)

• What is meant by effectiveness?
  • Cost effectiveness, cost exchange ratio, casualty exchange ratio, ROCE? Or all of these?
• In practice, it seems that effectiveness the degree of effect that one system has on another is not fixed
  • It varies throughout an engagement, for instance

6/1. It is now appropriate to use the GRM in its dynamic form:

• The three horizontal layers correspond to the Form Model, the Behavior Model, and Mission Management - part of Function Management. The other two oarts of Function Management (e.e., Resource Management and Viability Management) appear at left and right respectively, constituting yhe whole GRM in dynamic layered form, connected to the external world.
  • Note the similarlity to the three layer scheme of Technology, People, Process.
• Note that all separate land vehicles, UAVs, etc., treated as one system
• Valid - if we achieve organismic design
• However, different design options would introduce different values for many of the parameters. F'rinstance
• Battle damage might be greater with fewer, larger, concentrated vehicles. However...
• Battle damage repair might take much longer with more, widely dispersed vehicles
• Similarly, rearming and refueling on the go would be quite different for different options

• We don't know anything about our supposed enemy
• We don't know much about out own forces future beliefs and behaviors, training, etc.
• How can we possibly fill in the details necessary to make the simulation work sensibly?
• All true, but no reason to cop out
• First, and initially, it is sensible to assume that an enemy is neither inadequate, nor a giant in ten-league boots.
• It is sensible, as a start point, to assume that Red is as capable as Blue.
• Then, we can assume, too, that Red ethics, morals, behaviors, training, etc., are the same as Blue's, even if we are not too sure what Blue's are
• In the first instance, create Blue from your own designs, filling in parameter values from knowledge, experience or SWAG
• Employ appropriate, trusted weather and radio transmission models, typical Rx/Tx sensitivities & powers, and so on
• Having created Blue, replicate to create Red and couple so that the sensors and weapons of Blue seek Red and vice versa.
  • Run the model. First run should be a standoff, with both parties inflicting and receiving equal damage (e.g. averaged out over, say, 1,000 runs)
  • In a sense, the two interacting models operate like a Wheatstone Bridge (look it up!)
  • Things that we may not know about in both Blue or Red tend to cancel out
  • If we think,say, ethics, may be a showstopper, then we insert the same model element for ethics on both sides:
  • No difference. However...
  • Change Blue Ethics and the effects of "just and only" ethics on operational effectiveness may be observed
  • If it is minor, then ignore
  • If it is major, then we need to know, i.e., research!

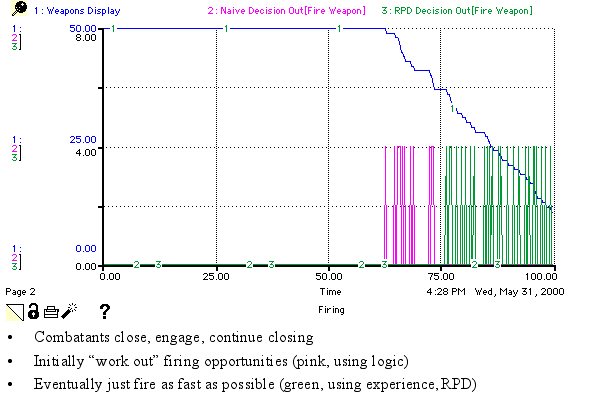
(RPD:Recognition Primed decision-making)

Return to SM Application Contents

• Establish a scenario
  • E.g. 2 identical land forces, 100m separation, engaging, weather
• Install identical technology
  • Radars, jammers, ESM, navigation, engines, weapons, situation displays, battle damage displays, formation control, maintenance, etc.
• Install identical people
  • Training, cognitive abilities, experience, learning capability, behavior, etc.
• Establish identical C2 processes
  • Assess situation, identify threats, etc.
• Make decisions engage, withdraw, fire, repair damage, etc.
• Underpin with comprehensive cost models
• Capital, maintenance, operating, damage repair, people, costs
• Identical forces engage, score identical results
  • Cost effectiveness, cost-exchange ratios, casualty exchange ratios
• Hold one force constant. Change only one item on other force, say active radar transmitter power
• Run model again
• Any difference in results due to single change
  • changing radar transmitter power makes difference to overall effectiveness (E)
  • in that scenario against that opposition
• Takes account of all interactions, dynamics, costs

Can optimize one force's technology

• Against given opposition in given scenario
• Vary performance of each component up, measure, down, measure and restore
• Repeat for all components install single change that made biggest increase in, say, cost effectiveness
• Repeat process until no further increase (20-30 cycles?)
• Process is cumulative selection.
• Result is optimum set of technologies,
• with ideal Mops = requirements?

The Interacting Blue Red Force Model becomes a test bed: what are

• Effects of training on Effectiveness?
• Can a smarter missile make up for not-so-smart operators/decision-makers?
• Effects on Effectiveness of increasing active radar power?
• Carrying more/less weapons
• Etc., etc.,

Possible to ratchet overall design, too.

• Far left shows cumulative selection of e.g., Blue fighter design, using enemy (Red) fighter threat as a dynamic reference
• When Blue fighter design has reach optimum, Blue fighter becomes seed for Red fighter cumulative selection
• Process can occur over several stages, with each design leapfrogging its predecessor
• Obvious dangers of creating non-feasible designs can be anticipated
• Insert physical/technological limits into offspring generation processes

Using nonlinear dynamic simulation, it is possible to update the basic systems engineering paradigm:

• To create hundreds, or even thousands of options covering different
  • vehicle arrangements: how many, what functionsÉ
  • operational parametersÉ power, capacity, sensitivity, range, frequency, etc., etc.
  • Support & logistics
  • Weapons performance, etc., etc.,
• To search through the resulting massive n-dimensional solution space efficiently and
• To find the optimum (e.g. most cost effective) solution of all the possible configurations
• To "prove" your solution is the right one.

The key is to use genetic algorithmic methods

• Establish pseudo-genes to code for parameters in solution system
• i.e., re-create the system solution from a set of genes,
• e.g., Gene A codes for "radar transmitter power"
• Gene A can take on a range of values that express as a range of transmitter powers
• e.g., Gene B codes for "number of weapons type X"
• Gene B can take on a range of values corresponding to the number of X missiles carried, with an upper limit set by capacity
• In each case, as the genes code for more or less, there is a consequent cost assessment
• E.g., more missiles carried = more cost
• E.g. greater missile Ph = less missile firings
• Design search starts by randomly generating a set of gene values
  • These vary the initial parameters in the Blue Model
  • These values determine a putative system design
    • number of vehicles, weapons, ranges, missile pH, etc.
• This system design solution is sent into combat against an unaltered, but still dynamic and interactive, Red force.
• The outcome of the conflict is recorded as e.g., the various forms of effectiveness provided by that particular set of genes
• The process is repeated for a significant number of random gene patterns
• Results from, say, 500 runs are compared and the "best" solution is recorded
• The corresponding gene values are set into the design as "radar transmitter power," "number of missiles," etc.
• This represents the first level of improved design
• The process is repeated, only now the extent by which the genes may change from the nominal value may be reduced
• The intent is to refine the "hill-climbing" process
• After a relatively few cycles the process is unable to improve Blue effectiveness
  • Typically, between 15 and 30 cycles
• The whole exercise may be repeated using different terrain and different Red opposition, until a firm, provable solution is established for all reasonable situations

The method is illustrated diagrammatically above.

A simplified example of the genetic/cumulative selection process follows.

In the following table, some 25 simulation runs have been recorded. Ony six genes have been used, to simplify the preesntation: they are

1. Blue Ph - probability of hit with a weapon, dimensionless
2. Blue Tx - radar transmitter power, in watts
3. Equipment quantity, referring to the number of weapons carried on a TLE
4. BD Crews - these are the number of battle damage crews, working on the move to repair damage to the SWARM
5. Decision Delay (firing) - refers to the time taken to decide to fire
6. Intelligence Transit time - the time taken for intelligence to be processed and presented to augment decision-making.

The six genes were chosen partly to illustrate the diversity of choice, and partly because, in the system under design, these genes represented sensitive parameters, i.e., small changes could make a significant difference.

So, the tables above show the various patterns of input variables - they represent 25 quite different designs. The tables below show the outcome from combat simulations, in which the design of Red is unchanged throughout, while it competes against 25 different Blue force designs.

Typical simulation run results are shown below, at the start of an optimization routine. Three different tabular results are shown below are for one set of 25 completed combat simulation runs. The results tables are for:

a) Blue Cost Effectiveness

b) Casualty Exchange Ratio

c) Blue cost effectiveness - Red cost effectiveness, i.e. the difference between them (this is a valid since Red and Blue are, initially, the same system).

So, to be clear, Run 3 below is one full simulation run in which Blue LF2020 engages in simulated combat in a particular terrain, with Red LF2020. In this series of 25 such runs, the particular measure has been taken at the end of each simulation run - during the course of the exchanges, the MOE values can fluctuate, as e.g., weapon systems are put out of action and as damage repair crews get things working again..

Other measures could have been included in the runs - it is simply a matter of choosing the desiring MOE, calculating it for each run and printing out the table.

In analyzing the results, as the arrows and comments show, all is not straightforward. The set of design genes that gave rise to run 3 - and therefore, design 3 - give maximum Blue Cost Effectiveness, and maximum Blue/Red Cost Effectiveness Difference; however, run 3 is far from best in terms of Casualty Exchange Ratio, and this is one of the fundamental issues surrounding LF2020. A variation on the simple approach would be to optimize around a composite MOE - some combination of Casualty Exchange Ratio and Cost Effectiveness, perhaps.

The optimization process is not complete, of course, as shown. One way to proceed would be to insert the gene values of Run 3 as the new start point, and repeat the procedure, obtaining 25 more runs, choosing the best (however chosen) and so on, until no further improvement is achieved. Clearly the overall process could be fully automated, without the need to stop and examine progress periodically.

The graph shows Cumulative Selection in operation. The x-axis represents a series of runs - in this example, 11 runs of 25 combat simulations each run. The results of this run are counterintuitive - they show Blue Cost Effectiveness rising as Blue Weapons Ready Stock rises. Investigation shows that it is possible to run out of weapons in a prolonged exchange, which would be expensive as the whole force could be lost.

In a second example, under the same conditions, it can be seen that Blue Cost Effectiveness is rising as Blue Weapons Ph rises; this is not surprising, as less weapons should be needed for the same effect. On the other hand, Blue cost Effectiveness is rising as Blue Radar Transmitter Power is falling. This is because lower radar transmitter power - provided the radar can still see the target - reduces the probability of being detected by Red Electronic Surveillance Measures (ESM). The simulation recognizes the inverse fourth power law for the active radar, and the inverse square law for the ESM. It is also true in this case that the lower power radar costs less.

Note:

1. This complete process is a powerful way of finding the optimum overall design, particularly as it measures the MOE of the whole system while it is in operation. In essence, however, it is no different from the standard Systems Engineering Problem-solving Paradigm, in that it generates criteria and trades optional solutions against them.
2. The idea of using a copy of Blue as the nonlinear interactive, dynamic reference during optimization has a number of additional advantages. Often, when seeking to model an opposing force, too little is known about such things as manning, training levels, morale, ethics, morals and belief systems, etc., all of which can have a material effect on outcome. Using a copy of Blue as reference, means that as much is known about Red as about Blue.

• The end result is a matched set of optimal parameters - specifications - for Blue, in the situation represented by the simulation
• It is a great advance on conventional methods
  
  • Matched specifications show each subsystem
    
    • making best contribution to overall Mission Effectiveness - however measured
    • while operating and interacting with other systems under operational conditions, i.e. organismic synthesis!
  • Solution system parameters contribute to optimum solution
    
    • not too little, not over the top, but…
    • just right for successful operations
  • Determines optimal support, maintenance, logistics, too

The optimization exercise, using a copy of Blue as Red, would be followed up by a series of further routines, using a variety of likely force structures as the interactive Red opponent.

• Had we been able to create a variety of terrains…
  …and given that the simulations were reasonable, then…
  We would have established
  
  • a systems solution,
  • a system design to the first level,
  • a set of research targets
  • a matched set of specifications for subsystems, and
  • a test bed upon which the incredulous—and future contractors—could explore, challenge, and possibly improve, our conclusions
• …and everything can be tracked back to the initial article, the TRIAD, and so on…

It works!

• Method used with great success in a variety of walks of life
• Essentially, nothing about the method that is context or technology dependent
• Used for Famine Relief, Reconstruction of Afghanistan, Global socioeconomic forecasting, and many, many more…

Systems Methodology Step 7 - Creating the Solution System

The final step concerns itself with the creation of tangible assets that, when brought together and activated, become the system solution to the original problem from Step 1.

At the end of Step 6, we had a matched an balanced set of specifications for Land Force 2020. This was to be an unprecedented system, at least in parts - nobody has yet, and may never, create such a system for such a purpose. However, to proceed with the demonstration of the Systems Methodology, see the following diagram.

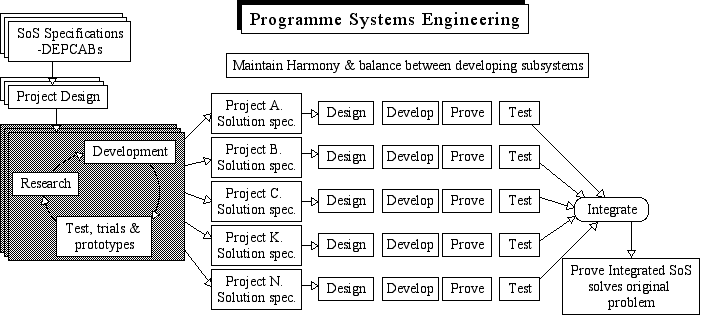
The SoS was comprised of several parts/subsystems, each candidates for separate projects:

• VSTOL Transport Aircraft
  • Teams of trained crews
  • Teams of trained C2 personnel
  • Command and Control facilities (C4I)
  • Remote piloting controls
  • Repair and Logistic Bays
• Land Transport Elements (TLEs - advanced vehicles)
  • Operating crews
  • Transmission systems
  • Hover systems
  • Sensor systems
  • Remote driving controls
  • UAV Launch and Recovery
  • Active Camouflage Systems (Chameleon and Photocopier)
• Raptor UAVs
  • remote pilot facilities
  • electromechanical avian capabilities
  • navigation
  • communications, internal and external
  • flight controls
    • flap, soar, stoop, evade, etc.
    • remote piloting
  • sensors (TV eyes, ESM, IR flash, laser etalons, etc.)
  • communications
  • weapon management systems
  • weapon delivery systems
  • energy accumulation, storage and distribution
  • etc.
• Dragonfly UAVs
  • as Raptor, but with flight controls relevant to dragonfly analogous behavior
  • etc.
• DTDMA/CNI System with associated Prime Mission functions:
  • Data sharing/ communications relay / image relay / video relay
  • Relative navigation
  • Identification
  • Cooperative reconnaissance
  • Cooperative identification
  • Target association
  • RASP formation
  • Cooperative target allocation
  • Cooperative kill assessment
  • Formation management and control
  • etc.
• Weapons
  • SREMP, the non-lethal short range electromagnetic pulse weapon to disable vehicles, electrical supplies, electronics, and communications
  • Other non-lethal weapons
  • CIWS - the close-on weapon system for TLE defense against weapons attack
  • etc., etc.

Notes:

1. Although some research will be needed in each of the areas identified in this list, some of it is within the range of short-term acquisition. For the raptors and dragonflies, for instance, it would be possible to develop working prototypes using model aircraft, model powered gliders and model helicopters. Some of their systems could be based on third generation mobile phones, which are soon to hit the market with 5Mpixel cameras and zoom lenses, and which can already send stills and video over sophisticated digital communication networks. It just needs some imagination!
2. So, although the complete SoS may not be in its final form until 2020, it could probably be fielded in less than complete, but nonetheless effective, form, using such prototype facilities, within 5 years of program start.
3. One aspect not addressed so far is the dynamic nature of the problem space. Problems can change so fast that, by the time a solution has been created, the problem has morphed out of recognition. This may render a SoS useless.
4. The answer? Well, there is little point in creating a useless solution to a no-longer existing problem..
   • Make the SoS highly adaptable, self-healing, and not too specific in its purpose.
   • Continually check the problem space and the symptoms throughout Steps 1 - 6 and on into Step 7, seeking both to update the final SoS proving criteria - see below - and to evolve the design in real time
   • Set up a continual design modification program so that the SoS is continually upgraded throughout its life

It soon becomes obvious that the full specifications for LF2020 cannot be met in all cases without some research and development. A suitable strategy for proceeding is presented in the figure above:

• Research and development is set in train for all the various project elements.
• Meanwhile, a set of independent projects is established under the overarching control of a central program team.
• The team establishes the objectives of each of the projects to match the set of specifications where appropriate.
• The strategy implicit in the figure above is to treat each of the projects as independent.
  • This is as distinct from the practice of developing software for all the projects in some central software facility. This practice disrupts the dedicated team ethic which helps to drive projects to an early and successful conclusion.
• Similarly, the strategy chooses not to insist upon the various projects using the same technological elements. In this instance, there is unlikely to be much common technology.

Another advantage of keeping the projects separate is that they do not impinge on each other, so that delays on one project need have no effect on the others. Further, if one project falls behind, them more effort can be directed towards it to restore the balance.

The risk from separate projects is that the developing subsystems/parts may suffer from specification "creep." To guard against this, program management must monitor the developing parts, particularly looking for any variations in DEPCABs (dynamic emergent properties, capabilities and behaviors.) The ideal method for such monitoring makes use of the simulation facilities developed in Steps 5 & 6. These will highlight any risks from potential DEPCAB variations, and may also be used to explore ways of rebalancing the design should variation become unavoidable...

The figure below shows one of the more technologically oriented sub-projects in some more detail, this time from a commercial, business viewpoint. Note that the top line, marked Concept, is a metaphor for the Systems Methodology, Steps 1 - 6.

Other views of systems engineering

The Systems Engineering 5-Layer Model

World Class Systems Engineering

Return to SM Application Contents

Derek Hitchins, 2005

http://www.hitchins.net